2024. 4. 1. 15:00ㆍ프로그래밍/java
요즘 "수학 리부트"란 책을 읽고 있다.
항상 수학과 영어가 부족하다고 느끼고 있었기 떄문에 항상 공부 해야지 해야지 하면서 미루고 있었는데 "OpenAPI와 스웨거를 활용한 실전 API 설계" 책을 다 읽고 때가 되었다고 생각했다.
서점에서 먼저 종이 책을 확인 한 후 이북으로 사서 출근 시간마다 보고 있는데 프로그래머를 위한 기초 수학을 설명해주고 있어서 매우 좋다!
시작은 논리식으로 시작해서 차근차근 공부하고 있다. 분명 대학교때 이미 배운 내용이고 지금까지 개발을 하면서 항상 써온 논리식이지만 기초를 다시 다지고 읽다 보니 지금까지 너무 주먹구구식으로 개발을 하고 있다는 느낌이 많이 들었다.
바로 내용으로 들어가 보자.
논리식 기호부터 한번 보자
| OR(논리합) | AND(논리곱) | NOT(부정) | XOR(베타적 논리합) | |
| 기호 | ∨ | ∧ | ¬ | ⊕ |
| 자바 코드 | || | && | ! |
위의 기호를 보면 a ∨ b 의 경우 코드로 옴겨보면 아래와 같다.

¬A ∧ B 는 의 경우는 아래와 같다.

이제 이 글의 핵시 내용인 드 모르간의 법칙(De Morgan's law)에 대해 설명 하겠다.
내용은 논리 연산에서 논리합은 논리곱과 부정기호로, 논리곱은 논리합과 부정기호로 표현할 수 있음을 가리키는 법칙
¬(a∨b) == ¬a∧¬b

¬(a∧b) == ¬a∨¬b

그냥 이렇게만 보면 머 그냥 그렇다고 느낄수도 있지만 복잡한 연산이 들어가면 달라진다.
(¬a∨b)∧¬(a∧b) 의 계산을 보자
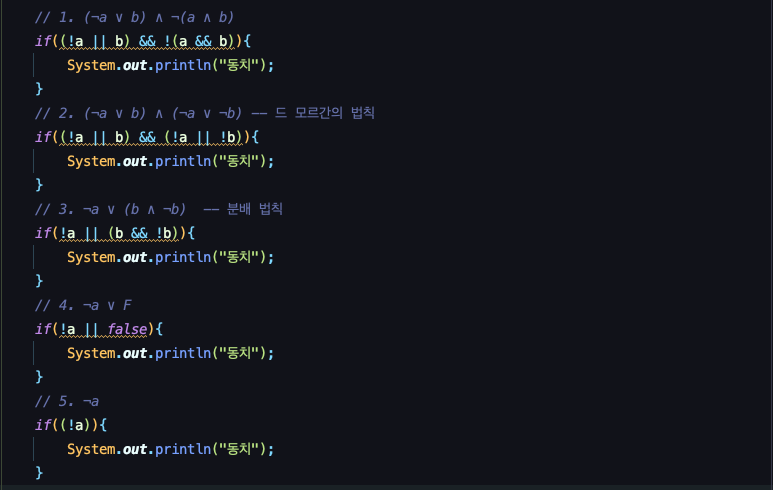
1번은 원복 식이다.
2번은 드 모르간의 법칙으로 변경되었다.
3번은 분배법칙으로 !a가 앞으로 나왔다.
4번은 !b AND b는 false밖에 나오지 않는다.
5번은 or조건의 경우 뒤의 false의 값은 무시해도 된다. 무조건 앞의 조건의 값을 따라간다.
4개의 조건문이 하나의 조건문으로 변경 되었다. 코딩을 하다보면 의외로 다중 조건문이 나올떄가 많으며 같은 조건을 또 계산하고 있느 ㄴ경우도 허다하다. 이는 코드의 분석도 어렵게 만들 뿐더러 유지보수하는데에도 난이도를 상승하게 만든다. 하지만 드 모르간의 법칙이랑 분배 법칙을 사용하여 최대한 다중 조건을 최소한 할수 있으면 코드가 더욱 깔금해 질것이다.
사실 인텔리 제이 같은 좋은 IDE 를 쓰면 자동으로 해주는 기능이다. 우리 모두 좋은 IDE를 쓰도록 하자..
안녕!
'프로그래밍 > java' 카테고리의 다른 글
| deep copy (0) | 2023.09.07 |
|---|---|
| redis를 이용해 중복 요청 막기 (0) | 2023.05.19 |
| Thread Method(1) (0) | 2023.05.09 |
| Java 멀티 스레딩 (2) | 2023.05.08 |
| facade layer (0) | 2023.05.03 |